2、匿名及递归函数

TOC

匿名函数

    匿名函数，顾名思义，就是一个没有标识符的函数，那么一个没有名字的函数，我们就称之为匿名函数，函数本身就是一个函数对象，其实我们给不给名字是无所谓的，我们也可以把一个函数对象给它放在列表当中，那么这个列表中的元素，遍历出来，通过索引访问，不需要名字也可以对其进行调用；

def func():
    pass
funcs=[func]
del func
print(funcs[0]) # <function func at 0x102c2c048>
# 匿名函数的实现
print([lambda x, y: x + y]) # [<function <lambda> at 0x10292c048>]

lambda函数的实现

    在有些场景下，我们只是临时使用一下函数，并不会出现反复使用的情况，那么这个时候使用我们的匿名函数就非常合适了，不仅节省内存的利用率，也实现了语法的简洁，使用匿名函数的时候，我们需要用到一个关键字，即lambda，它用来定义匿名函数，而且lambda一般都是一次使用，所以不建议定义标识符，如choice=lambda x, y: x if x > y else y，不建议定义一个choice，而且lambda表达式只能写在一行上，也称为单行函数，lambda表达式，往往会被我们用来高阶函数的传参当中，也就是高阶函数需要我们传递一个函数进去，其实在之前使用过，sorted函数它有过参数是key，之前传的str也是一个函数；

# 其实对于sorted的key也可以使用lambda函数来实现；
print(sorted([1,2,'5','v','a'],key=lambda x:str(x))) # [1, 2, '5', 'a', 'v']
# 利用三元表达式的优化实现，如果是字符串就使用其所在ASCII码中的十进制来比较
print(sorted([1,2,'5','v','a'],key=(lambda x:x if isinstance(x,int) else ord(x) ))) # [1, 2, '5', 'a', 'v']

    lambda表达式就是，在lambda关键字后面写参数列表，然后接上一个冒号，冒号后面给定一个表达式，表达式只能有一个，且不能出现赋值语句，同时也不能出现return语句；
    语法：lambda args1[,args...] : result_expression  # 需要注意的是，result_expression只能有一个，当然，我们也可以写三元表达式，还有一点需要注意，不可以在冒号后面出现等号，不能写赋值表达式，lambda函数执行完成之后会得到一个函数，和def定义都函数没什么区别，都是函数；

print((lambda x, y: x + y)(1, 2))  # 使用括号可以把lambda函数优先级提升，将其提升为一个函数，后面接一个括号()就是执行该函数；
# 三元表达式案例
lambda x, y: x if x > y else y
# 利用lambda定义一个无参无返回值的函数
lambda:None

lambda函数默认值

    lambda表达式的形参也支持默认值，直接在定义的时候直接给定其默认值就行了，但是，和def定义的函数一样，我们要注意它的引用类型；

print((lambda x=1, y=2: x + y)()) # 3

lambda函数keyword-only参数

    上面说过了，我们的lambda函数实际上和我们的def定义的函数是一摸一样的，没有任何区别，所以它也支持关键字参数；

print((lambda x, *, y: x + y)(1,y=2)) # 2

lambda参数收集

    lambda函数也支持我们的参数收集，包括位置参数、关键字参数，但是需要注意的是，我们的lambda函数只支持一个返回值；

print((lambda *args,**kwargs: [kwargs,args])(1,2,y=2,x=2)) # [{'x': 2, 'y': 2}, (1, 2)]

lambda惰性求值

    lambda表达式也可以结合我们的生成器表达式，来实现惰性求值，每当调用的时候，就返回一个值；

print((lambda *args:( x%2 for x in args))(*range(10))) # <generator object <lambda>.<locals>.<genexpr> at 0x105038200> #返回一个生成器对象，也是一个可迭代对象
# 结合列表解析式
print([i for i in (lambda *args:( x%2 for x in args))(*range(10))]) # [0, 1, 0, 1, 0, 1, 0, 1, 0, 1]

lambda结合高阶函数

    如下两个案例是结合了高阶函数map的使用用法，比较复杂，可以仔细看看，理解一下，加深对lambda的使用技巧；

print([x for x in (lambda *args: map(lambda x: x + 1, args))(*range(5))])
# [1, 2, 3, 4, 5]
print([x for x in (lambda *args: map(lambda x: (x + 1, args), args))(*range(5))])
# [(1, (0, 1, 2, 3, 4)), 
#  (2, (0, 1, 2, 3, 4)), 
#  (3, (0, 1, 2, 3, 4)), 
#  (4, (0, 1, 2, 3, 4)), 
#  (5, (0, 1, 2, 3, 4))]

递归函数

    递归算法和栈都有后进先出这个性质，基本上能用递归完成的算法都可以用栈完成，都是运用后进先出这个性质，每个函数的每一次调用都会创建一个独立都栈桢(Stack Frame)，哪怕是递归，同一个函数调用；

堆和栈

    堆和栈其实就是程序的内存分配方式，在C语言中，当一个程序被加载到内存中运行，系统会为该程序分配一块独立的内存空间，并且这块内存空间又会再被细化分为很多区域，比如栈区、堆区、静态区、全局区，在Java、C#或者Python对于内存回收，有一个GC机制，有了GC机制之后，我们就完全不需要去管内存是如何分配如何回收的，而在C语言里面，程序员是需要自己进行内存的分配和回收的；
    栈区，一般用来保存局部变量，定义在函数内部的局部变量都保存在栈区，存储在栈区的变量，在函数执行结束后，会被系统自动释放；

函数与栈

    上面说过，函数调用完成之后，它内部的局部变量都会销毁，这就是栈的表现，这也就是为什么函数有作用域的原因，因为那些局部变量都是放在栈中的，函数调用完成，栈就会被销毁，此次函数调用结束，这也就是为什么说每次函数调用结束，该函数所创建的局部变量等信息都会进行销毁的原因，函数的形参等信息都是放在栈当中的，所以我们可以认为函数是一个封装，它可以调用无数次，函数可以复用，但这无数次的调用都是没有关系的，因为他们是不同但栈；
    那么函数的执行是与栈相关的，栈是后进先出的一个数据结构，我们也可以理解它是一个后进先出的一个队列，那么函数的执行过程就和栈的压栈有关，上面说了，每一个函数都会创建一个栈桢，就是每一次函数执行都会事先将和函数相关的数据增加到栈里面去，这称之为入栈或者进栈，我们在需要使用到这些函数的时候，会从栈里面取出数据，这个称之为出栈；
    这个栈里面就包含了这个函数运行的相关信息，比如局部变量，比如形参，这些局部变量都要进行压栈，每一个函数，都是如此，那么对于某一个函数来说，它的某一次调用，都会创建一个独立都栈并且将其压栈，哪怕是同一个函数，同一个函数在调用多次的时候，比如递归，两个函数我们可以片面的认为他们两个是没有任何关系的，不严格；

递归函数

    递归的定义就是，函数直接或者间接调用自身，我们将这种调用，就称之为递归调用，递归函数一定是要有边界的，虽然函数按道理来讲是可以无限次调用自身，但是如果一个函数要无限次调用的话，按照上述的函数执行过程，一个函数的调用是和栈相关的，栈的空间大小是有限的，栈是内存空间，所以递归也必须做有限次调用，所以递归是有边界条件的；
    也就是说，递归函数需要有两个条件，第一个递归前进段，第二个递归返回段，也就是说递归能进去，也能出来，当边界条件不满足的时候，递归前进，也就是函数不满足条件继续调用，当边界条件满足时，递归返回，也就是满足条件时不在继续调用，开始返回，逐层返回，前进段就说计算的过程，返回段就是拿到结果的过程，计算时，逐层深入，求结果时，逐层返回；

def foo():
    return foo()
foo()
# RecursionError: maximum recursion depth exceeded
# 可以看到，当我们在进行递归调用的时候，如果没有给定边界，那么就会抛出上述异常，这实际上是说，函数的栈太大了，当一个栈用，存在当压栈函数过多的时候，Python会直接抛出异常，因为Python默认对递归的深度进行了限制，避免栈溢出，可以使用sys.getrecursionlimit获取；

求斐波那契数列

    拿斐波那契数列为例，可以看到，如下使用了一个三元表达式的方式来进行编写的，斐波那契数列的第1个数为1，第二个数也数1，所以当n为1和2时，值为1，因此得出以下公式；

def fib(n):
    return 1 if n < 3 else fib(n - 1) + fib(n - 2)
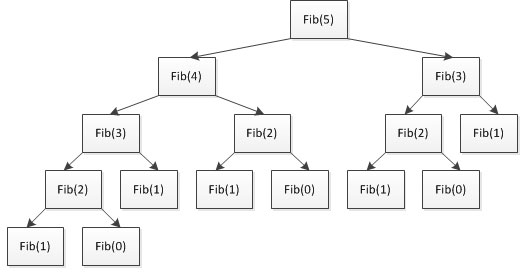
print(fib(6)) # 8

流程分析

    假定n为4时，根据函数首次执行的数fib(n - 1) + fib(n - 2)，首先执行的是fib(n - 1) ，当fib(n - 1)这个递归完成之后，才会执行fib(n - 2)这个递归，当两次结果都拿到之后，才能拿到最终都值，详细分析如下图；

    当所有递归压栈完成，然后等拿到结果之后，依次返回；

性能问题

    可以看到，递归的一次递归带来的函数压栈调用太多，当我们要求一个100的斐波那契数列的时候，利用这个递归函数会发现非常非常慢，压栈的深度太深，而且还有大量的重复计算，这是在使用递归的时候遇到的非常常见的问题，所以递归能不用则不用，递归主要是让我们去理解函数的调用过程，具体流程也可通过http://pythontutor.com/visualize.html#mode=edit该网站查看；

性能优化

    当我们使用for循环来实现斐波那契数列的时候，会发现速度非常之快，那么我们使用上面的这个递归来实现会发现这个速度极慢，因为其压栈的深度非常深，而且计算量非常巨大，而且Python递归的深度是有限制的，递归会进行反复的压栈和出栈，所以栈内存是很容易溢出的；
    递归实际上是有多种写法的，一种是上面这样，美得像公式一样，但是很有可能会出现性能问题，还有一种就是类似循环一样，将一个循环封装成一个可递归的函数，递归一层一层的调，相当于循环一层一层的循环；
    如下就是类似循环一样的优化版本，这个版本的斐波那契数列递归，大量的减少了函数压栈的过程，也省去了大量的重复计算的过程；

def fib(n, a=0, b=1):
    a, b = b, a + b
    if n == 1:
        return a
    return fib(n - 1, a, b)
print(fib(4)) # 3

间接递归调用

    简介递归调用，就是通过别的函数调用了自身的函数，如果构成了循环调用那就非常危险了，因为函数就是一种封装，也就是说函数里面是怎么写的，我们是不清楚的，也不可能为了写一个功能将所有的函数全部看一遍，每一个函数都可能套函数，函数套函数，各种调用，我们也很难逐一把函数了解得清清楚楚，所以编写代码时要有清晰的思考，避免循环调用；

def f1():
    f2()
def f2():
    f1()
f1()

递归总结

    递归是一种很自然的表达，它像数学公式一样，符合我们的逻辑思维，但是递归相对运行来讲，效果比较低下，每一次函数调用都要开辟栈桢，所以递归压栈和出栈清栈空间的过程是非常耗时的，递归也有深度的限制，如果递归层次太深，函数反复压栈，栈内存很容易溢出，所以递归的调用也不易过深，所以尽量避免递归的使用；