TOC
数制
其实我们日常生活中常用的数字,它就是数制的一种表示方法,世界上第一台计算机采用的是十进制表示法,当冯诺依曼加入研究小组就发现,采用十进制会有非常多是弊端,所以当它进行第二台计算机,就提出并且使用了二进制,那么从此之后,我们的计算机就都开始采用了二进制来表示计算机当中所有的信息;
因为我们的开关,有接通和断开,电压有高和低、电容有充和放,这些状态都是两种状态,这两种状态,我们刚好可以使用0和1来表示,所以相对于0和1,使用在计算机上更加的合适,换一种说法相对于十进制来说,二进制在物理上更容易实现,只有1和0这两种状态,他们不容易产生数据的紊乱,或者说错误,所以说,采用二进制还有可靠性强的好处;
数制基础概念
数码:数码其实就是表示进制所用的数字,比如二进制,那么二进制是数码为0和1,八进制呢,那就是0、1、2、3、4、5、6、7,这些就是数码;
数位:数位以下面的实际表示为例,那么5643.52的数位就是,次方好反过来,也就是3210-1-2这就是数位,小数点前的数字从后往前从0开始,小数点后面的数字从前往后从-1开始,数位一般用i来表示;
基数:可以看到,下面的实际表示法都是10的多少次方,这就是基数,因为下面的数字是十进制,所以十进制的基数就是10,所谓基数就是表示该进制所用的数码的个数,那么十进制的的数码各位为10个,所以十进制的基数位10,以此类推二进制的基数位2,基数一般用R来表示;
位权:位权表示,这一位数它所占据的权利有多大,以下面的实际表示法为例,基数的数位次方就称之为维权,比如5它的位权在千位上,所以它的位权就是1000,只是写成了基数的数位次方,所以十进制就是10^i,二进制就是2^i,八进制则是8^i,十六进制就是16^i,其实也可以写成R^i;
示例数字:5643.52
= 5 x 1000 + 6 x 100 + 4 x 10 + 3 + 5 x 0.1 + 0.02 x 0.01 # 正常换算
= 5 x 10^3 + 6 x 10^2 + 4 x 10^1 + 3 x 10^0 + 5 x 10^-1 + 2 x 10^-2 # 利用次方的形式的实际表示法
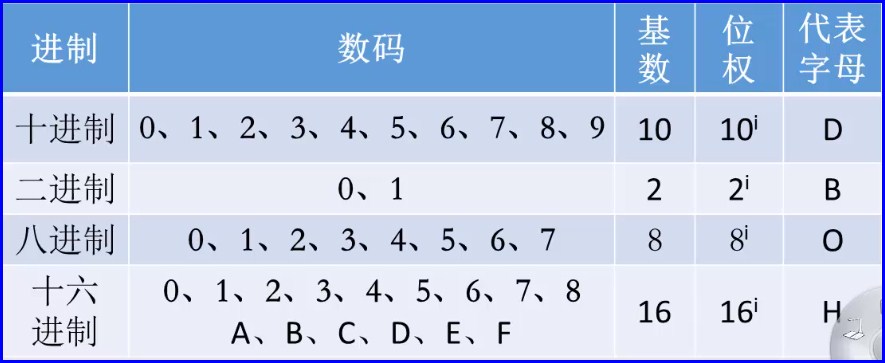
进制英文表示法
对于不同的进制,它都有自己的不同的英文表示法,这个在学习开发语言的人是非常重要的,可能会涉及到ASCII码的操作,具体如下;
十进制(D):对于十进制它的英文表示法为D;
二进制(B):对于二进制它的英文表示法为B;
八进制(O):对于八进制它的英文表示法为O;
十六进制(H):对于十六进制它的英文表示法为H;
进制转换
进制转换会涉及到二进制、八进制、十进制和十六进制之间的相互转换,其实十进制转换各个进制是有一定的方法的,十进制数作为被除数,转换为什么什么就是除数,一直往下除,当商为0,则得到的的余数,倒着写就是该十进制转为指定进制的数字;

十进制转为其他进制
如下是十进制转其他进制的法则;
十进制转二进制,整数部分除2取余,商为0则结束,余数倒着写(如果有小数,小数部分乘2取整,小数为0结束,整数顺着写,此为整除法);
十进制转八进制,整数部分除8取余,商为0则结束,余数倒着写(如果有小数,小数部分乘8取整,小数为0结束,整数顺着写,此为整除法);
十进制转十六进制,整数部分除16取余,商为0则结束,余数倒着写(如果有小数,小数部分乘16取整,小数为0结束,整数顺着写,此为整除法);
整数进制转换
整数进制转换使用,取余法,余数倒着写的方式,示例如下;
# 求十进制9的二进制
2 |_9_ 1 # 余数
2 |_4_ 0
2 |_2_ 0
2 |_1_ 1
0
# 即 9(2)=1001
# 求十进制77的八进制
8 |_77_ 5 # 余数
8 |_9_ 1
8 |_1_ 1
0
# 即 77(8)=115
# 求十进制77的八进制
16 |_77_ 13 # 余数,在十六进制中 A表示10,B表示11,C表示12,D表示13
16 |_4_ 4
0
# 即 77(16)=4d
小数进制转换
整数进制转换使用,整除法,整数顺着写的方式,示例如下;
# 将0.54这个十进制数字,转换成二进制
0.54 x 2 = 1.08 # 取整 1
0.08 x 2 = 0.16 # 取整 0
# 可以看到,十进制数字0.54有两位小数,所以我们的结果也取两位小数即可,小数顺这些,即 0.54(2)=0.10
# 将0.54这个十进制数字,转换成八进制
0.54 x 8 = 4.32 # 取整 4
0.32 x 8 = 2.52 # 取整 2
# 可以看到,十进制数字0.54有两位小数,所以我们的结果也取两位小数即可,小数顺这些,即 0.54(8)=0.42
# 将0.54这个十进制数字,转换成十六进制
0.54 x 16 = 8.64 # 取整 8
0.64 x 16 = 10.24 # 取整 10
# 可以看到,十进制数字0.54有两位小数,所以我们的结果也取两位小数即可,小数顺这些,即 0.54(16)=0.8a
合并转换
下面就展示,如果一个十进制数字既有小数部分,也有整数部分,如何转为二进制、八进制和十六进制;
# 将45.62这个十进制数字,转换成二进制,又有整数,又有小数,那么就得分开计算
2 |_45_ 1 # 余数
2 |_22_ 0
2 |_11_ 1
2 |_5_ 1
2 |_2_ 0
2 |_1_ 1
0
# 即,45的数字,转为二进制则为 101101
# 将0.62这个十进制数字,转换成二进制
0.62 x 2 = 1.24 # 取整 1
0.24 x 2 = 0.48 # 取整 0
# 可以看到,十进制数字0.62有两位小数,所以我们的结果也取两位小数即可,小数顺这些,即 0.62(2)=0.10
# 即,45.62(2)=101101.10
其他进制转为十进制
上面已经说了十进制转为其他任何进制的方法,那么下面就说下其他进制转为十进制,其他进制转为十进制则使用位权法则;
示例数字:5643.52
= 5 x 1000 + 6 x 100 + 4 x 10 + 3 + 5 x 0.1 + 0.02 x 0.01 # 正常换算
= 5 x 10^3 + 6 x 10^2 + 4 x 10^1 + 3 x 10^0 + 5 x 10^-1 + 2 x 10^-2 # 利用次方的形式的实际表示法
可以看到5的基数是10,数位是3,基数和数位合并起来10^3就是位权,我们将每一位的数字乘位权,然后加起来就得到了十进制数字本身,这种方法就称为位权法;
对于十进制是上面这样的,那么对于二进制、八进制、十六进制我们只需要把基数换一下就行了;
二进制转十进制(位权法)
方法:按位乘以权值相加
注意:整数数位为正,从右往左,从0开始,小数为负,从左往右,从-1开始
二进制转十进制
# 将数字 1011.01(2)转为十进制数字
整数部分:从右往左,从0开始
1的数位为0
1的数位为1
0的数位为2
1的数位为3
小数部分:从左往右,从-1开始
0的数位为-1
1的数位为-2
即:1011.01=3210.-1-2
# 根据上面的法则,换一下基数
1 x 2^3 + 0 x 2^2 + 1 x 2^1 + 1 x 2^0 + 0 x 2^-1 + 1 x 2^-2
= 8+2+1+0.25
= 11.25(10)
# 八进制、十六进制转十进制都是一样的
信息编码
人熟悉的语言有很多,比如数字1,2,3...,比如符号,A、#、?...,比如汉语中、英、法,但是计算机只认识0和1,现在我们想让计算机来存储和处理他们,所以我们就必须让计算机能够理解他们,所以我们就需要将这些信息转换成计算机能够识别的0和1就可以了;
所以我们要将这些信息转换成计算机能够识别的0和1,这一个过程,我们就称之为编码,这个编码就分为我们常用的数字、符号以及汉语等类型;
信息编码
计算机的信息编码原则就是使用二进制来表示,文字和符号,分类就分为数字编码、字符编码和汉子编码;
数字编码
数字有正数字和负数字,但是计算机底部识别的是0和1,他们不能够识别我们正整数和负整数,所以我们也可以将正数符号和负数符号用0和1来表示,所以计算机就将0表示正数1表示负数;
现在有符号之后就又要进行划分了,我们数字就划分成有符号数和无符号数,因为计算机最小存储单元为4k,也就是8bit,那么一个8位的二进制数,有符号数和无符号数,的取值范围是多少,那么对于取值范围,我们又要进行分析;
假设我们有一个八位数,这八位数我们现在如果是无符号数,那么这八位就全部用来表示数字,由于没有符号,所以全部都应该是正数,我们二进制当中可以表示最大的数字就是1,所以当这八位全部为1的时候,即为最大数,那么转换成十进制就是255,那么它为正整数的取值范围则为0-255,也就是2的n次方-1,2^n-1;
# 无符号
一个八位数最大:1 1 1 1 1 1 1 1 = 255 = 2^8-1
一个八位数最小:1 1 1 1 1 1 1 1 = 0
# 有符号(有符号第一位为符号位),1代表负数,0代表正数
一个八位数最大:1 0 0 0 0 0 0 0 = 127 = 2^7 -1
一个八位数最小:0 1 1 1 1 1 1 1 = -128 = -2^7

